Journal of Clinical & Experimental Orthopaedics

Keywords

Dynamic MRI; Knee kinematic; Flexion-Extension-Axis, Tibio-femoral joint

Introduction

Dynamic measurement of knee joint kinematics is a helpful tool because it aids in clinical diagnostics [1-3] helps understand sport injury mechanisms [4,5] and is essential in developing implant designs and alignment techniques [6,7]. Movement and load transmission are the main function of the knee joint. Reconstructive surgery and partial or total knee arthroplasty aim to restore the pretraumatic or normal kinematics and load transmission when these have been affected by injury or disease. Assessing normal knee motion is of substantial interest for improving joint health [3,8-10].

The knowledge of normal knee kinematics has been extensively studied and has experienced a paradigm shift. The theory of the instant center of motion postulates that the femoral condyles are not circular, which results in an axis-around which the tibia flexes and extends–that moves with knee flexion and extension (=instant center of motion) [11,12]. This theory also assumes that the axes around which the tibia and patella flex and extend are exactly parallel to the anatomic coronal plane, which is defined by morphological landmarks and not by the motion of the knee. The principle of the instant center of motion derives from analyzing the geometry of the femoral condyles in the anatomical sagittal plane and dates back to the late 19th century [11]. However, with the support of improved imaging modalities the kinematic theory has seen a fundamental revision of the concept of the axes of motion of the knee, which has implications for component design and alignment in total knee arthroplasty. The theory of the instant center of motion was challenged and it was postulated that the axes around which the tibia and patella flex and extend are several degrees offset from the anatomic coronal plane [12,13]. It was also postulated that if the axes were offset from the anatomical coronal plane it would result in two separate fixed femoral axes around which the tibia and the patella flex and extend. Proof of this postulation was established in 1993 [14]. Improved imaging technology and computer simulation provided further evidence [15,16]. These two axes are not parallel to the anatomic coronal plane or to the transepicondylar axis but are perpendicular to the flexion-extension plane of the knee [17,18]. However, within the orthopaedic community the belief in the instant center of motion theory persists in the current age. The identification and exact localization of the two fixed axes around which the tibia and patella flex and extend can be facilitated with dynamic magnetic resonance imaging (MRI).

MRI is a useful non-invasive diagnostic modality to identify intraarticular soft tissue injuries and osseous stress reaction [19]. In addition, dynamic MR imaging of the knee with both high spatial and temporal resolution and high signal-to-noise ratio (SNR) will offer substantial improvements [20]. Compared to static imaging (or passive loading followed by static imaging), the complex muscle activation pattern that occurs during movement is better represented in dynamic imaging (as the leg is in motion). Dynamic imaging has the potential to characterize and quantify mechanics of internal structures in vivo [21].

Several studies related to dynamic imaging of human knee have been carried out to characterize movements of bones in the knee using MRI [4,22-26]. However, the motion is quasi-static, in that the knee is imaged at fixed angles and not in continuous motion. There have been studies that image knee in motion, but they exhibit limited spatio-temporal resolutions due to limitations in coils or associated hardware [27,28].

This study demonstrates the advantage of a dedicated RF array coil together with a movement device to perform dynamic imaging of cadaver knees with a high spatio-temporal resolution at 1.5 T. The goal of this study was 1) to establish a setup for dynamic MRI knee measurements using a 16 channel RF coil array and a movement device, 2) generate a knee model with a cadaver knee to facilitate a 3-dimensional characterization of knee kinematics and 3) generate a mathematical algorithm to calculate a defined and fixed axis around which the tibia flexes and extends.

Methods

The choice of this specific receive array coil for this application involves consideration of the following aspects:

1. Region of interest, dimensions and geometry of the cadaver knee.

2. Shape of coil housing adapted to the cadaver leg.

3. Signal-to-noise ratio (SNR) at the region of interest (ROI).

4. Applicability of acceleration (partially parallel acquisitions).

It was essential to allow an unobstructed and uniform movement of the cadaver knee during the acquisition of the MR signal. The geometry of the coil fits well to the cadaver knee/leg and provides high sensitivity, SNR and parallel imaging capabilities. The coil and its housing had the following dimensions and characteristics: a semicircular surface of 160 mm inner diameter and a length of 180 mm that covers the whole knee and allows having 16 array coil elements on three sides of the knee as close as possible to the region of interest. The fourth side of the knee is open to allow knee motion. Thus, during the whole motion the knee is covered as much as possible by the coil and an optimum filling factor is achieved at all positions.

To guide the movement of the cadaver knee during the measurements and to perform a reproducible motion during the whole acquisition, a dedicated movement device was used (Figure 1). The device consisted of two baseplates of acrylic glass connected with a hinge. The device was driven by a pneumatic piston which was powered by pressurized air from a compressor via a pressure limiter. The inflow and outflow of air were adjusted per the desired speed of the movement. The range of motion was adjusted by two photoelectric sensors defining the upper and lower turning points. A third photoelectric sensor provides an external trigger signal to synchronize the movement device with the MR acquisition.

Figure 1: The movement device used to guide the cadaver knee through range of motion; The movement device consisted of two baseplates connected with a hinge; Driven by a pneumatic piston inside a pneumatic cylinder the movement device enabled a range of motion of 45°; Adjusting the cadaver knee between measurements increased the cumulative range of motion to 90°; The coil was centered at the hinge.

The dynamic images were acquired using the Magnetom Avanto MRI Scanner (Siemens Healthcare GmbH, Erlangen) and a segmented multi-slice FLASH sequence (TE=2.38 ms, TR=5.0 ms, BW=416 Hz/pixel, flip angle=60°, in-plane resolution=1.41 × 1.41 mm², slice thickness=3 mm, 32 slices, 4 segments, approx. 25-30 time frames, total acquisition time approx. 8-10 min).

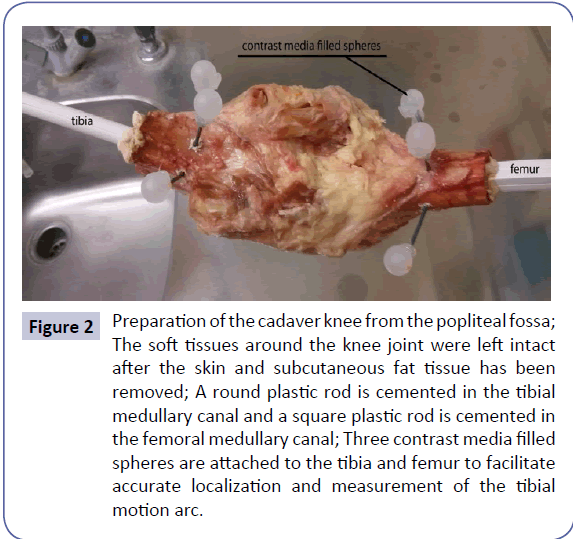
Ten knee specimens were thawed, dissected, aligned, and potted in preparation for dynamic MRI measurements. The thigh was transected 20 cm proximal to, and the lower leg was transected 15 cm distal to the joint line of the knee. Soft tissues between 15 cm proximal to and 12 cm distal to the joint line of the knee were retained with exception of the skin and the subcutaneous fatty tissue (Figure 2).

Figure 2: Preparation of the cadaver knee from the popliteal fossa; The soft tissues around the knee joint were left intact after the skin and subcutaneous fat tissue has been removed; A round plastic rod is cemented in the tibial medullary canal and a square plastic rod is cemented in the femoral medullary canal; Three contrast media filled spheres are attached to the tibia and femur to facilitate accurate localization and measurement of the tibial motion arc.

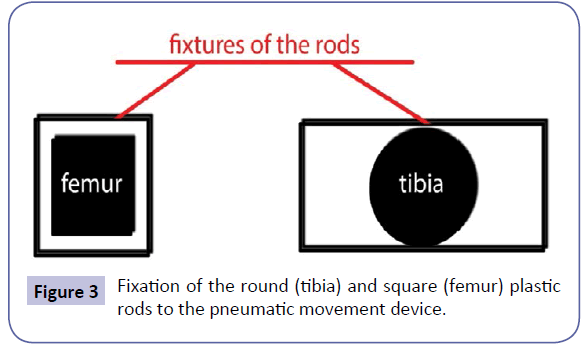
Plastic intramedullary rods were cemented into the medullary canals of the femur and tibia using methyl methacrylate (Palacos©; ZimmerBiomet). The femoral rod was square, the tibial rod was round. The rods were attached to alignment fixtures that were connected to the movement device. The femoral rod fixture was square with the inner diagonal matching the outer diagonal of the femoral rod. The tibial rod fixture was rectangular with the inner height matching the diameter of the tibial rod and the width three times the diameter of the tibial rod (Figure 3).

Figure 3: Fixation of the round (tibia) and square (femur) plastic rods to the pneumatic movement device.

This fixation allowed for translation, rotation and varus/valgus angulation of the tibia during range of motion. Using a functional alignment procedure, the position and orientation of the femur and tibia were adjusted using the alignment fixtures until the flexion-extension axis of the tibiofemoral joint were aligned with the flexion-extension axis of the hinge of the movement device. Six contrast media filled spheres were attached to the femur and tibia via thin plastic rods (to extend the motion range of the spheres), three to the femur and three to the tibia, to facilitate accurate 3-dimensional localization of the femur and tibia during motion (Figure 2).

Mathematical Analysis

To identify the flexion-extension axis the contrast media filled spheres attached to the femur served as a relative coordinate system. This 3-dimensional coordinate system consisted of an axial plane (=internal/external rotation), sagittal plane (flexion/ extension), and coronal plane (varus/valgus angulation). The three contrast media filled spheres attached to the tibia moved within this relative coordinate system of the femur.

The following algorithm was used to calculate the flexionextension axis:

Define the 3-dimensional relative coordinate system of the femur at each point of time during range of motion and transform all coordinates of the three tibial contrast media filled spheres into this coordinate system.

Find the optimal plane for each of the tibia spheres over the motion cycle.

Project each of the three tibial spheres within its “sagittal” plane. The normal vector of each plane defines the direction of the related flexion-extension axis.

Calculate the center of each circle defined by the motion of the tibial spheres within each “sagittal” plane by applying circular interpolation. Deviation of any tibial sphere from the sagittal plane by internal/external rotation is compensated by the mathematical algorithm.

Calculate the mean of the three normal vectors and find the point with the lowest distance to all three axes. This averaged vector together with the nearest point defines the flexion-extension axis.

Each measured position of the tibial contrast media filled sphere at any time point was compared to the ideal position based on the calculated flexion-extension axis (=nonlinear curve optimization). The error between the measured position and the nonlinear curve optimization was calculated and expressed in the Euclidean norm:

The variable yi is the ideal sphere position of the measured sphere position xi , n is the number of points (3 × (number of spheres) × (number of time points)).

Results

The knee movement device generated a range of motion arch of 45°. Repositioning the cadaver knee in the movement device in between measurements permitted visualization of a motion arch of up to 90° in the dynamic MRI scan. All knee specimens had intact ligamentous structures, no meniscal pathology, and no osteoarthritic changes of the cartilage surface (Video 1). The six contrast media filled spheres attached to the femur and tibia were easily visible on the dynamic MRI scan and facilitated precise localization of the femur and tibia and calculation of the path of motion (Video 2).

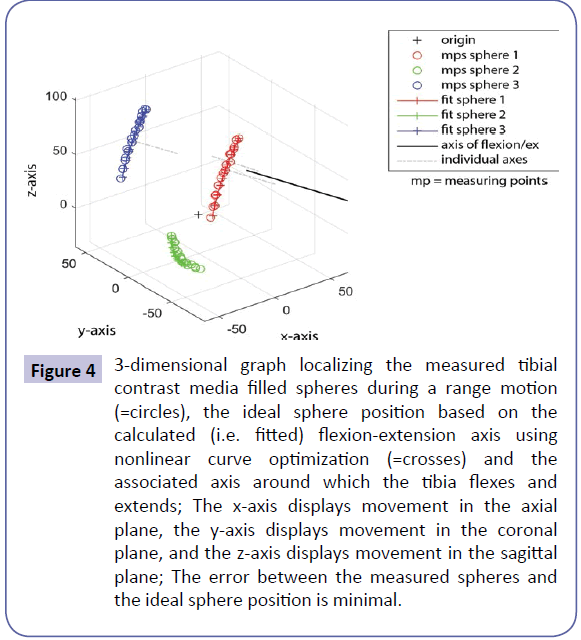
A fixed axis around which the tibia flexes and extends was localized in all ten specimens. The three tibial contrast filled spheres produced concentric arcs within the femoral relative coordinate system (Figure 4). Nonlinear curve optimization for the three arcs for all ten knees disclosed an error as low as F=7.8 [mm].

Figure 4: 3-dimensional graph localizing the measured tibial contrast media filled spheres during a range motion (=circles), the ideal sphere position based on the calculated (i.e. fitted) flexion-extension axis using nonlinear curve optimization (=crosses) and the associated axis around which the tibia flexes and extends; The x-axis displays movement in the axial plane, the y-axis displays movement in the coronal plane, and the z-axis displays movement in the sagittal plane; The error between the measured spheres and the ideal sphere position is minimal.

Discussion

Normal knee motion is still discussed with different interpretations of the results [29]. It has been thought to occur about a variable flexion-extension axis (=instant center of rotation) [3]. This variable flexion-extension axis was thought to be perpendicular to the sagittal plane. However, the investigations leading to this conclusion assumed that the axes of tibial flexion and extension around the femur are perpendicular to the anatomical sagittal plane [14]. Our study introduces a new technique to assess knee motion with dynamic MRI. We present a novel passive movement device that generates repetitive, periodic knee motion, a cadaveric knee model that allows reliable localization and interpretation of knee kinematics, and a mathematical algorithm that enables the calculation of the axis around which the tibia flexes and extends.

Several limitations related to this study should be discussed. First, our study used a cadaveric knee model. Although these cadaveric knees had no traumatic or degenerative changes and the geometry of the cadaver knees did not differ from knees of living subjects, the results of this study should be verified with human subjects. Second, our study investigated the path of motion of tibia around the femur during passive range of motion. Active range of motion and range of motion under load may demonstrate a different motion pattern in regards to internal and external rotation and translation of the tibia [23]. However, the localization of the axis around which the tibia flexes and extends is based on osseous distal femoral geometry and therefore should not be affected by active or passive range of motion [15]. Additional studies using the technology presented in this study will further enlighten this question. Third, attaching three contrast media filled spheres to each the femur and tibia is an invasive technique and not applicable for use in living human subjects. The goal of this study was to establish a movement device, an imaging protocol, a knee model, and a mathematical algorithm leading to precise measurements of knee kinematics. Using the localization of the axis around which the tibia flexes and extends as an established concept of knee motion confirmed the accuracy of our methods [14,29]. Further studies in humans will refrain from using the contrast media filled spheres. Instead anatomical bony landmarks in the tibia and femur as previously demonstrated will serve as reference points [28].

In comparison to other studies using “dynamic” MRI, our protocol permits the visualization of the complete arch of motion at any point of time. The dynamic element of previous “dynamic” MRI studies have used a static MR scan at different degrees of knee flexion, termed quasi-static [22,23]. The optimized receive array coil used in the present study along with the designed movement device has been shown useful in acquiring images at very fine spatial and temporal resolutions in a 1.5 T MR scanner. However, our MRI sequence requires the repetition of the same movement through several cycles. Deviation from the same movement leads to motion artifacts that can affect the accuracy of the measurement. The designed movement device inhibits such deviation and guarantees a repetitive motion sequence. The movement device is also applicable to use in living humans and enables passive range of motion as well as guides active range of motion. Further studies are under way to evaluate the presented technique in living subjects. Our data is in agreement with previously published data and confirm the presence of a fixed axis around which the tibial flexes and extends [14,15,29]. The low calculated error of F=7.8 [mm] confirms that our experimental setup was accurate and precise in localizing the flexion-extension axis.

Conclusion

Our study introduces a novel technique of using dynamic MRI to visualize knee kinematics. Using the passive movement device that generates repetitive knee motion, the cadaveric knee model, and the mathematical algorithm generates an accurate system that enables precise calculation of knee motion. Additional in vivo studies will further assess the applicability of this experimental setup.

Funding

This study was funded by institutional resources only.

References

1. Draper CE, Santos JM, Kourtis LC, Besier TF, Fredericson M, et al. (2008) Feasibility of using real-time MRI to measure joint kinematics in 1.5T and open-bore 0.5T systems. J Magn Reson Imaging 28-1: 158-166.
2. Fellows RA, Hill NA, Gill HS, MacIntyre NJ, Harrison MM, et al. (2005) Magnetic resonance imaging for in vivo assessment of three-dimensional patellar tracking. J Biomech 38-8:1643-1652.
3. Freeman MA, Pinskerova V (2005) The movement of the normal tibio-femoral joint. J Biomech 38-2: 197-208.
4. Defrate LE, Papannagari R, Gill TJ, Moses JM, Pathare NP, et al. (2006) The 6 degrees of freedom kinematics of the knee after anterior cruciate ligament deficiency: an in vivo imaging analysis. Am J Sports Med 34-8: 1240-1246.
5. Draper CE, Besier TF, Santos JM, Jennings F, Fredericson M, et al. (2009) Using real-time MRI to quantify altered joint kinematics in subjects with patellofemoral pain and to evaluate the effects of a patellar brace or sleeve on joint motion. J Orthop Res 27-5: 571-577.
6. Benoit DL, Ramsey DK, Lamontagne M, Xu L, Wretenberg P, et al. (2007) In vivo knee kinematics during gait reveals new rotation profiles and smaller translations. Clin Orthop Relat Res 454: 81-88.
7. Brossmann J, Muhle C, Schroder C, Melchert UH, Bull CC, et al. (1993) Patellar tracking patterns during active and passive knee extension: evaluation with motion-triggered cine MR imaging. Radiology 187-1: 205-212.
8. Nha KW, Papannagari R, Gill TJ, Van de Velde SK, Freiberg AA, et al. (2008) In vivo patellar tracking: clinical motions and patellofemoral indices. J Orthop Res 26-8: 1067-1074.
9. O'Donnell P, Johnstone C, Watson M, McNally E, Ostlere S (2005) Evaluation of patellar tracking in symptomatic and asymptomatic individuals by magnetic resonance imaging. Skeletal Radiol 34-3: 130-135.
10. Pinskerova V, Johal P, Nakagawa S, Sosna A, Williams A, et al. (2004) Does the femur roll-back with flexion? J Bone Joint Surg Br 86-6: 925-931.
11. Bugnion E (1892) Le mechanism du genou. In: Viret-Genton IC, ed. Extrait due recueil inaugural de l'Univeristie Lausanne. Lausanne.
12. Smidt GL (1973) Biomechanical analysis of knee flexion and extension. J Biomech 6-1: 79-92.
13. Soudan K, Van Audekercke R, Martens M (1979) Methods, difficulties and inaccuracies in the study of human joint kinematics and pathokinematics by the instant axis concept. Example: the knee joint. J Biomech 12-1: 27-33.
14. Hollister AM, Jatana S, Singh AK, Sullivan WW, Lupichuk AG (1993) The axes of rotation of the knee. Clin Orthop Relat Res 290: 259-268.
15. Eckhoff DG, Bach JM, Spitzer VM, Reinig KD, Bagur MM, et al. (2005) Three-dimensional mechanics, kinematics, and morphology of the knee viewed in virtual reality. J Bone Joint Surg Am 87 Suppl 2: 71-80.
16. Coughlin KM, Incavo SJ, Churchill DL, Beynnon BD (2003) Tibial axis and patellar position relative to the femoral epicondylar axis during squatting. J Arthroplasty 18-8: 1048-1055.
17. Eckhoff D, Hogan C, DiMatteo L, Robinson M, Bach J (2007) Difference between the epicondylar and cylindrical axis of the knee. Clin Orthop Relat Res 461: 238-244.
18. Brar AS, Howell SM, Hull ML (2016) What are the bias, imprecision, and limits of agreement for finding the flexion-extension plane of the knee with five tibial reference lines? Knee.
19. Sadineni RT, Pasumarthy A, Bellapa NC, Velicheti S (2015) Imaging Patterns in MRI in Recent Bone Injuries Following Negative or Inconclusive Plain Radiographs. J Clin Diagn Res 9-10: TC10-13.
20. Raghuraman S, Schrauth JH, Weber DL, Resmer F, Haddad-Weber M, et al. (2013) Dynamic MR imaging of a minipig's knee using a high-density multi-channel receive array and a movement device. MAGMA 26-2: 215-228.
21. Draper CE, Besier TF, Fredericson M, Santos JM, Beaupre GS, et al. (2011) Differences in patellofemoral kinematics between weight-bearing and non-weight-bearing conditions in patients with patellofemoral pain. J Orthop Res 29-3: 312-17.
22. Dragoo JL, Phillips C, Schmidt JD, Scanlan SF, Blazek K, et al. (2010) Mechanics of the anterior interval of the knee using open dynamic MRI. Clin Biomech (Bristol, Avon) 25-5: 433-437.
23. Johal P, Williams A, Wragg P, Hunt D, Gedroyc W (2005) Tibio-femoral movement in the living knee. A study of weight bearing and non-weight bearing knee kinematics using 'interventional' MRI. J Biomech 38-2: 269-276.
24. Patel VV, Hall K, Ries M, Lindsey C, Ozhinsky E, et al. (2003) Magnetic resonance imaging of patellofemoral kinematics with weight-bearing. J Bone Joint Surg Am 85-A-12: 2419-2424.
25. Patel VV, Hall K, Ries M, Lotz J, Ozhinsky E, et al. (2004) A three-dimensional MRI analysis of knee kinematics. J Orthop Res 22-2: 283-292.
26. Witonski D, Goraj B (1999) Patellar motion analyzed by kinematic and dynamic axial magnetic resonance imaging in patients with anterior knee pain syndrome. Arch Orthop Trauma Surg 119-1-2: 46-49.
27. Barrance PJ, Williams GN, Snyder-Mackler L, Buchanan TS (2006) Altered knee kinematics in ACL-deficient non-copers: a comparison using dynamic MRI. J Orthop Res 24-2: 132-140.
28. Sheehan FT, Zajac FE, Drace JE (1998) Using cine phase contrast magnetic resonance imaging to non-invasively study in vivo knee dynamics. J Biomech 31-1: 21-26.
29. Smith PN, Refshauge KM, Scarvell JM. (2003) Development of the concepts of knee kinematics. Arch Phys Med Rehabil 84-12: 1895-1902.